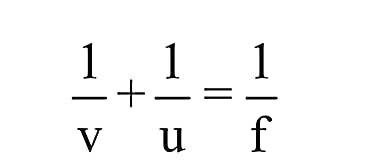Magnification in Hindi
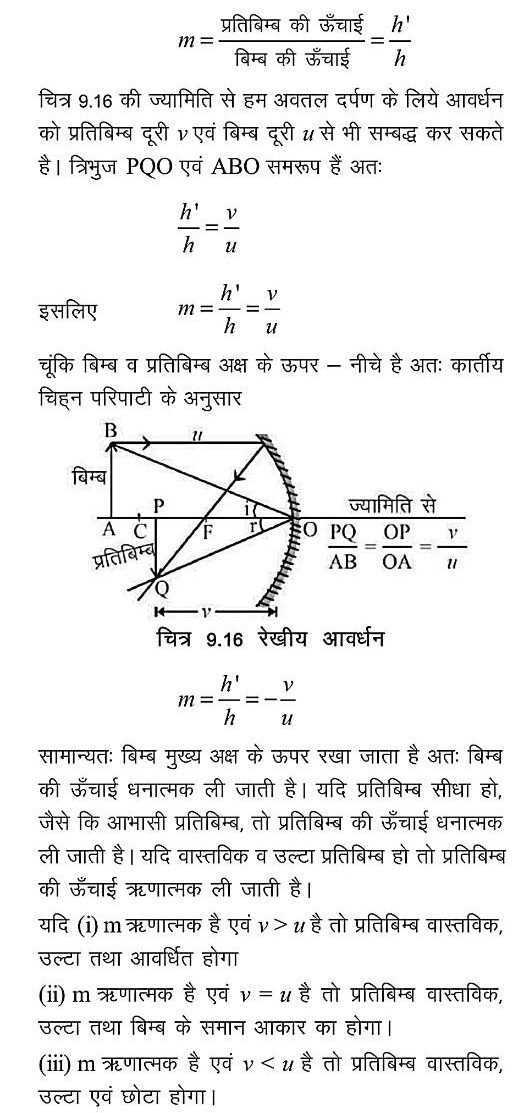
- प्रतिबिम्ब की ऊँचाई एवं बिम्ब की ऊँचाई के अनुपात को आवर्धन कहा जाता है | समान्यत: इसे m से दर्शाया जाता है
- इससे हमें यह ज्ञात होता है कि किसी बिम्ब का प्रतिबिम्ब बिम्ब से कितना गुना आवर्धित है। दर्पण द्वारा किसी बिम्ब को आवर्धित करने की क्षमता ही आवर्धनता कहलाती हैं ।
- यदि बिम्ब की ऊँचाई h हो एवं प्रतिबिम्ब की ऊँचाई h’हो तो गोलीय दर्पण से उत्पन्न आवर्धनता
Magnification in Hindi


Magnification in Hindi FAQ –
1. निम्न में से कौनसे दर्पण में वृहद दृष्टि क्षेत्र दिखेगा
(क) समतल दर्पण
(ख) उत्तल दर्पण
(ग) अवतल दर्पण
(घ) परवलियक दर्पण
Click to show/hide
2. प्रकाश का वेग सर्वाधिक होगा
(क) पानी में
(ख) कांच में
(ग) निर्वात में
(घ) ग्लिसरीन में
Click to show/hide
3. किस प्रभाव के कारण टंकी के पेंदे पर रखा सिक्का थोड़ा ऊपर उठा हुआ दिखाई देता है
(क) अपवर्तन
(ख) परावर्तन
(ग) पूर्ण आन्तरिक परावर्तन
(घ) इनमें से कोई नहीं
Click to show/hide
4. यदि एक दर्पण की फोकस दूरी + 60 सेमी. है तो यह दर्पण होगा
(क) अवतल दर्पण
(ख) परवलिय दर्पण
(ग) समतल दर्पण
(घ) उत्तल दर्पण
Click to show/hide
5. एक समतल दर्पण की फोकस दूरी होगी
(क) 0
(ख) 1
(ग) अनन्त
(घ) इनमें से कोई नहीं
उत्तर ⇒ ???????
प्रश्न 1. जब कोई वस्तु प्रकाश के सभी रंगों को अवशोषित कर लेती है तो वह वस्तु हमें किस रंग की दिखाई देगी?
उत्तर- वह वस्तु हमें काली दिखाई पड़ती है।
प्रश्न 2. यदि हम समतल दर्पण में हमारा पूर्ण प्रतिबिम्ब देखना चाहें तो दर्पण की न्यूनतम लम्बाई कितनी होनी चाहिये ?
उत्तर- किसी व्यक्ति का पूरा प्रतिबिम्ब देखने के लिए उस व्यक्ति की लम्बाई की आधी लम्बाई का समतल दर्पण चाहिए।
प्रश्न 3. उत्तल दर्पण के कोई दो उपयोग लिखिये।
उत्तर-
- उत्तल दर्पण में बड़ी वस्तुओं के छोटे प्रतिबिम्ब प्राप्त करके सजावट के लिए उपयोग में लेते हैं।
- इनका उपयोग सामान्यतः वाहनों के पश्च दृश्य (wing) दर्पणों के रूप में किया जाता है।
प्रश्न 4. अवतल दर्पण के कोई दो उपयोग लिखिये।
उत्तर-
- बड़ी फोकस दूरी का अवतल दर्पण हजामत बनाने के लिए प्रयोग किया जाता है, जिससे व्यक्ति के चेहरे का आभासी, बड़ा और सीधा प्रतिबिम्ब बनता है।
- अवतल दर्पण परावर्तक दूरदर्शी में काम में लेते हैं। इससे दूरदर्शी की विभेदन क्षमता में वृद्धि होती है।
प्रश्न 5. दर्पण सूत्र लिखिये।
उत्तर- ध्रुव से बिम्ब की दूरी u, ध्रुव से प्रतिबिम्ब की दूरी v एवं ध्रुव से फोकस दूरी f ये तीनों राशियाँ एक समीकरण द्वारा सम्बद्ध हैं जिसे दर्पण सूत्र कहा जाता है।